9. Matplotlib: visualización gráfica¶

9.1. ¿Qué es Matplotlib?¶

Matplotlib es una librería Python que permite generar gráficas estáticas, animadas e interactivas.

9.2. De Matplotlib, Jupyter y las gráficas mostradas¶

En todo este capítulo se asumirá que las siguientes líneas de código han sido ejecutadas, previamente, para cada porción de código:

import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline

Sí usted ejecuta Python/Matplotlib dentro de un entorno diferente a Jupyter, deberá evitar colocar la instrucción %matplotlib inline y en su lugar colocar la instrucción plt.show() al final de cada código, para que se le muestren las gráficas correspondientes.

9.3. Una primera aproximación¶

Una de las características de Matplotlib es la facilidad con la que se puede comenzar a trazar gráficas, vea el siguiente código:

plt.plot([5,10,6,-10,15,1])

[<matplotlib.lines.Line2D at 0x20e71272748>]

La linea anterior produce la gráfica mostrada en la figura, a la función plot únicamente se le pasó como argumento una lista de valores numéricos. Un resultado un poco más trabajado se obtiene con el siguiente código:

plt.plot([0,1,2,3,4,5], [5,10,6,-10,15,1], 'r--o', label="Partícula 1")
plt.xlabel("Tiempo (s)")
plt.ylabel("Posición (m)")
plt.title("Una primera aproximación")
plt.text(2,7,"$ P_1 (2,6) $", color="b")
plt.legend()
plt.grid(ls="--", color="#dadada")

Se puede observar que aquí se adicionan elementos descriptivos: etiquetas, leyendas y anotaciones, que usualmente sirven para describir completamente una información que se proporciona a través de las gráficas.

9.4. La función `plot`¶

La función plot está contenida en el módulo pyplot y básicamente con esta se produce cualquier gráfica bidimensional en coordenadas rectangulares. Esta función soporta varias maneras de ejecutarla dependiendo la cantidad de argumentos que se pasen.

La forma más básica de la función plot es pasarle un sólo argumento, por ejemplo:

plt.plot([1,2,1,0,-1,1])

[<matplotlib.lines.Line2D at 0x20e71461e80>]

Al pasarle un sólo argumento, este se toma como los valores de la coordenada vertical, y se asume que la horizontal varía de 0 a N-1, donde N es el número de elementos contenidos en la lista de valores que se introducen.

La sintaxis más habitual es introducir dos argumentos, donde el primero contiene una lista X que define los valores de la coordenada horizontal, y el segundo una lista Y correspondiente a los valores de la coordenada vertical, por ejemplo:

plt.plot([10,25,30,60,70,100], [100,200,-100,300,0,-250])

[<matplotlib.lines.Line2D at 0x20e714bbf98>]

9.4.1. Graficando funciones matemáticas¶

En matemáticas, una función es una relación que asigna elementos de un conjunto de manera unívoca a otro conjunto. Usualmente una función matemática se puede representar mediante una gráfica en coordenadas cartesianas, colocando uno de los conjuntos en el eje horizontal y el otro en el vertical.

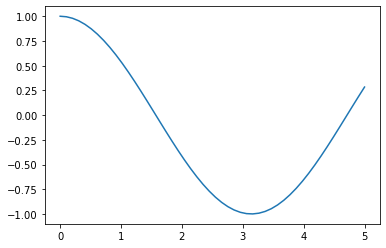
Utilizando Python, y de manera específica la librería NumPy, se pueden evaluar las funciones matemáticas en un intervalo determinado y en una cantidad finita de puntos. Por ejemplo, suponga que se requieren calcular todos los pares ordenados correspondientes a la función \( y = \cos x \) en el intervalo \( 0 \leq x \leq 5 \), en Python se tendría que definir como:

x = np.linspace(0,5)
y = np.cos(x)

Las variable x es un arreglo de NumPy que contiene 50 valores linealmente equiespaciados entre 0 y 5, la variable y es también un arreglo de NumPy que resulta de aplicar la función coseno a cada valor de x. Si se quiere graficar lo anterior, entonces, utilizando plot:

plt.plot(x, y)

[<matplotlib.lines.Line2D at 0x20e7151e400>]

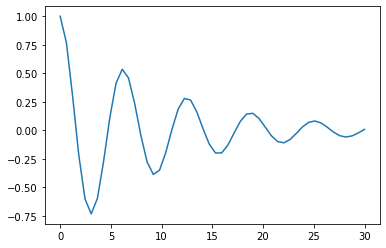
De manera similar a lo anterior se procederá a definir y graficar la función \(y = e^{-0.1x} \cos x \) en el intervalo \( 0 \leq x \leq 30 \):

x = np.linspace(0, 30)
y = np.exp(-0.1*x)*np.cos(x)
plt.plot(x,y)

[<matplotlib.lines.Line2D at 0x20e7154f2e8>]

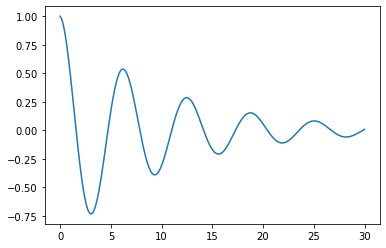
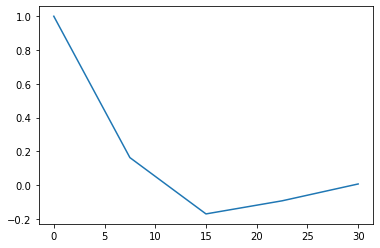
La cantidad de puntos a evaluar es una cuestión muy importante, ya que de esto depende la correcta visualización del comportamiento de una función. Naturalmente, entre más puntos evaluados mejor será la apreciación que se tenga de la curva en cuestión, pero implica un mayor gasto de memoría para guardar y evaluar todos los datos. Enseguida se muestra la misma función graficada en el mismo intervalo pero con 1000 y 5 puntos evaluados de manera respectiva, notará la diferencia entre los casos, es evidente que en el caso de los 5 puntos se pierde muchísima información.

# Con 1000 puntos evaluados
x = np.linspace(0, 30, 1000)
y = np.exp(-0.1*x)*np.cos(x)
plt.plot(x,y)

[<matplotlib.lines.Line2D at 0x20e71562898>]

# Con 5 puntos evaluados
x = np.linspace(0, 30, 5)
y = np.exp(-0.1*x)*np.cos(x)
plt.plot(x,y)

[<matplotlib.lines.Line2D at 0x20e715c19b0>]

9.4.2. Modificando el color, estilos y grosor de línea¶

La función plot acepta argumentos adicionales que sirven para modificar y controlar las características de la línea que se grafica. Por ejemplo, se puede pasar un tercer argumento que contenga una combinación de color y estilo de línea:

x = np.linspace(0, 30)
y = np.exp(-0.1*x)*np.cos(x)
plt.plot(x, y, "r--")

[<matplotlib.lines.Line2D at 0x20e716320f0>]

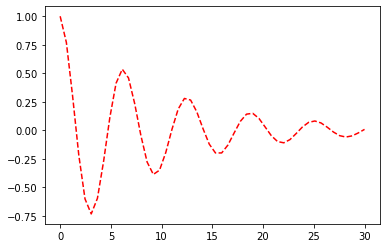
El código anterior genera una gráfica con una línea en color rojo (r) y un estilo de línea discontinua (--).

Si en lugar del string -- se coloca go, se obtiene una gráfica como la mostrada enseguida, podrá inferir que g refiere al color verde (green) y o justamente al uso de este caracter como símbolo para representar cada punto.

x = np.linspace(0, 30)
y = np.exp(-0.1*x)*np.cos(x)
plt.plot(x, y, "go")

[<matplotlib.lines.Line2D at 0x20e71692cc0>]

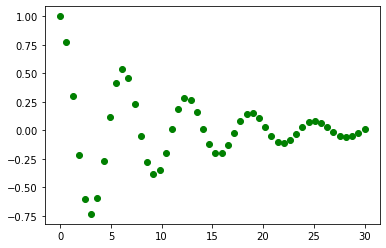
En https://matplotlib.org/api/markers_api.html se muestra una tabla con los símbolos (markers) disponibles para utilizar en la función plot. En https://matplotlib.org/api/colors_api.html puede consultar información respecto a los colores que puede abreviar mediante un sólo caracter.

Además de la forma anterior, también es posible especificar el color y estilo de línea utilizando keyword arguments, por ejemplo:

x = np.linspace(0, 30)
y = np.exp(-0.1*x)*np.cos(x)
plt.plot(x, y, linestyle="--", color="r")

[<matplotlib.lines.Line2D at 0x20e726d1978>]

En ambos casos se especifica un cierto estilo de línea y color, con la diferencia notoria de la sintaxis.

Utilizar keyword arguments es una manera más general, puesto que la definición con strings no funciona para los casos en que se requieren colores que no se pueden especificar con un sólo caracter, por ejemplo, Matplotlib dispone de un color llamado coral y este no puede ser invocado mediante un sólo caracter, hace falta escribir todo el nombre.

x = np.linspace(0, 30, 80)
y = np.exp(-0.1*x)*np.sin(x)
plt.plot(x, y, linestyle="-", color="coral", marker="*")

[<matplotlib.lines.Line2D at 0x20e72740630>]

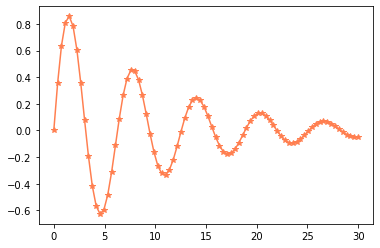
El grosor de línea se puede controlar mediante el keyword argument linewidth, por ejemplo;

plt.plot(x, y, linestyle="-", color="coral", marker="*", linewidth=3)

[<matplotlib.lines.Line2D at 0x20e727a3e48>]

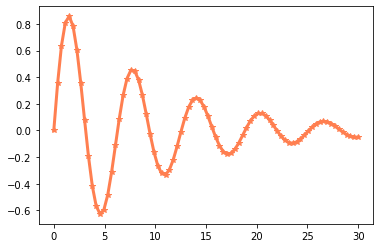
La función plot soporta algunos keyword arguments acortados. Por ejemplo, se puede utilizar ls en lugar de linestyle, lw en lugar de linewidth, ms en lugar de markersize, mfc en lugar de markerfacecolor, entre otros.

9.5. Título de gráfica, etiquetas de ejes y nombres de curvas¶

Por su naturaleza las gráficas nos sirven para presentar y/o visualizar información de ciertos datos, para lo cual se hace necesario especificar información descriptiva de lo que se muestra. Es muy común que se agreguen etiquetas a los ejes horizontal y vertical, así como el nombre de gráfica. Además, si se está graficando más de una curva, se hace necesario especificar a qué refiere cada una de ellas.

Por ejemplo, observe el siguiente código y la gráfica producida:

x = np.linspace(0, 30, 500)
y1 = np.exp(-0.1*x)*np.cos(x)
y2 = np.exp(-0.2*x)*np.sin(x)
plt.plot(x, y1, "b-", label="Partícula 1")
plt.plot(x, y2, "r-", label="Partícula 2")
plt.xlabel("Tiempo (s)")
plt.ylabel("Posición (mm)")
plt.title("Gráfica de posición")
plt.legend()

<matplotlib.legend.Legend at 0x20e7280dc88>

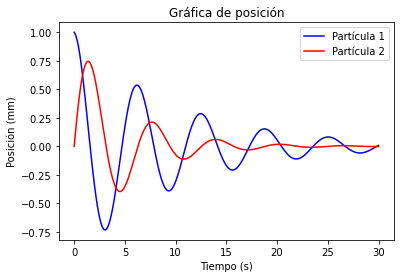
La instrucción xlabel coloca una etiqueta al eje horizontal, de manera similar ylabel lo hace para el eje vertical. Con title adicionamos un título a la gráfica. La instrucción legend sirve para colocar el recuadro con el nombre asignado a cada curva mediante el keyword argument label.

9.6. Anotaciones¶

Con anotaciones nos referimos a cualquier texto que se coloque dentro del Axes de Matplotlib. Usualmente utilizadas para indicar ciertas características partículares en una gráfica, o bien alguna nota informativa al respecto. La función base para realizar este tipo de tareas es text. La sintaxis más simple de text es:

plt.text(px, py, texto)

Donde px y py denotan las coordenadas en donde se colocará la anotación indicada en texto. Veamos un ejemplo:

x = np.linspace(0, 30, 100)
y = np.exp(-0.1*x)*np.cos(x)
plt.plot(x, y, "m")
plt.xlabel("Tiempo (s)")
plt.ylabel("Posición (mm)")
plt.title("Gráfica de posición")
plt.text(10, 0.5, "Algo informativo")

Text(10, 0.5, 'Algo informativo')

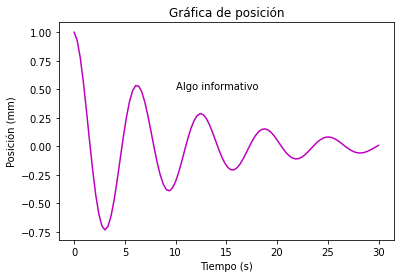
Note que únicamente colocamos el texto Algo informativo dentro del gráfico, de manera más específica en las coordenadas (10,0.5).

Al texto colocado podemos darle formato y ajustarlo a nuestros requerimientos, para ello a la función text se le pueden incluir los keyword arguments descritos en https://matplotlib.org/users/text_props.html. Por ejemplo:

x = np.linspace(0, 30, 200)
y = np.exp(-0.1*x)*np.cos(x)
plt.plot(x, y, "m")
plt.xlabel("Tiempo (s)")
plt.ylabel("Posición (mm)")
plt.title("Gráfica de posición")
plt.text(10, 0.5, "Algo informativo", fontsize=16, color="r", 
         name="Times New Roman")

Text(10, 0.5, 'Algo informativo')

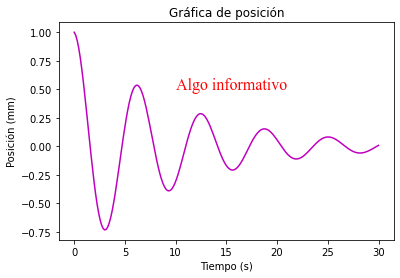
Observe que lo único que se cambió fueron algunas propiedades del texto, tales como el tamaño de la fuente con fontsize, el color de fuente con color y el tipo de fuente con name, con este último se debe tener cuidado, dado que el nombre de la fuente indicada debe estar instalada en la PC que se ejecuta.

9.7. Gráficas en coordenadas polares¶

Las coordenadas polares o sistema de coordenadas polares son un sistema de coordenadas bidimensional en el que cada punto del plano se determina por una distancia y un ángulo * . Habitualmente las funciones en coordenadas polares tienen la forma \( r = f(\theta)\).

En Matplotlib se dispone de la función polar, la cual traza una gráfica en coordenadas polares, dados como argumentos tanto la variable independiente \(\theta\) como la función \(r\). Enseguida vamos a ver cómo graficar la tan conocida rosa polar, cuya ecuación general está dada por:

\[ r = a \cos\left( k\theta + \phi_0 \right) \]

Implementando esto en Python, se tiene:

theta = np.linspace(0, 2*np.pi, 1000)
a,k,phi0 = 5,7,0
r = a*np.cos(k*theta + phi0)
plt.polar(theta, r, "r")

[<matplotlib.lines.Line2D at 0x20e6e895cc0>]

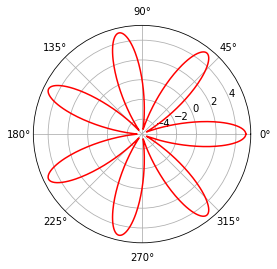
Observe que la función polar funciona de manera bastante similar a plot, de hecho se le pueden pasar los mismos keyword arguments para personalizar el gráfico resultante.

9.8. Gráficas de barras¶

9.9. Gráficas de pastel¶

Las gráficas de pastel (o de tarta, o gráficos circulares) nos sirven para representar porcentajes y proporciones. Matplotlib dispone de la función pie, cuya sintaxis depende del grado de personalización y control que se requiera sobre la gráfica de pastel a dibujar.

Para ejemplificar el uso de esta función vamos a suponer que se tienen los siguientes datos sobre algunas personas que tienen cierta cantidad de manzanas en su poder:

Nombre	Manzanas
Ana	20
Juan	10
Diana	25
Catalina	30

Para representar el porcentaje del total del cual dispone cada uno, podemos trazar una gráfica de pastel. Para ello realizamos lo siguiente:

manzanas = [20,10,25,30]
nombres = ["Ana","Juan","Diana","Catalina"]
plt.pie(manzanas, labels=nombres);

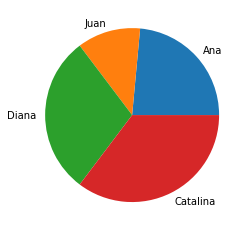
Observe que lo primero que hacemos es importar la librería matplotlib, enseguida, en utilizando listas definimos los nombres y el número de manzanas correspondientes. Luego, la función pie acepta un primer argumento que contiene los valores absolutos de cada ítem, además, de un keyword argument labels que contiene las etiquetas correspondientes.

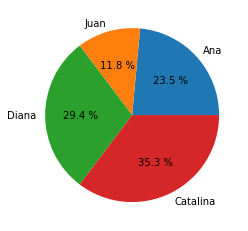
El porcentaje correspondiente a cada ítem se puede indicar mediante el argumento autopct:

manzanas = [20,10,25,30]
nombres = ["Ana","Juan","Diana","Catalina"]
plt.pie(manzanas, labels=nombres, autopct="%0.1f %%");

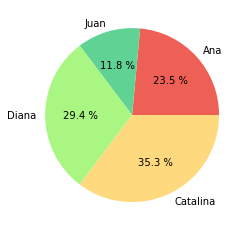
Los combinación de colores se puede especificar de manera manual, pasando una lista de color en formato hexadecimal o RGB.

manzanas = [20,10,25,30]
nombres = ["Ana","Juan","Diana","Catalina"]
colores = ["#EE6055","#60D394","#AAF683","#FFD97D","#FF9B85"]
plt.pie(manzanas, labels=nombres, autopct="%0.1f %%", colors=colores);

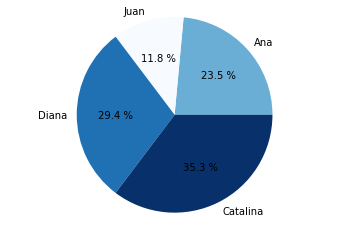
Los colores también se pueden determinar y autocalcular utilizando un mapa de color específico. Enseguida se muestra un ejemplo donde la variación es sobre colores en tonos azules.

from matplotlib import cm
from matplotlib import colors

manzanas = [20,10,25,30]
nombres = ["Ana","Juan","Diana","Catalina"]

normdata = colors.Normalize(min(manzanas), max(manzanas))
colormap = cm.get_cmap("Blues")
colores =colormap(normdata(manzanas))

plt.pie(manzanas, labels=nombres, autopct="%0.1f %%", colors=colores)
plt.axis("equal");

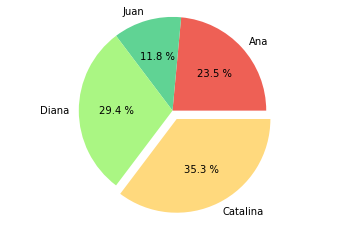
Es posible también segmentar o separar del bloque una o más de las rebanadas de la gráfica de pastel. Para ello se debe pasar una lista o tupla con valores entre 0 y n que indican el desfase respecto al centro, 0 indica ningún desfase y n un desfase equivalente a n*r, donde r es el radio de la gráfica de pastel.

manzanas = [20,10,25,30]
nombres = ["Ana","Juan","Diana","Catalina"]
colores = ["#EE6055","#60D394","#AAF683","#FFD97D","#FF9B85"]
desfase = (0, 0, 0, 0.1)
plt.pie(manzanas, labels=nombres, autopct="%0.1f %%", colors=colores, explode=desfase)
plt.axis("equal");

9.10. La función `subplot`: múltiples axes¶

La función subplot sirve para insertar axes en un figure organizados de una manera predefinida, usualmente una cuadrícula de m filas y n columnas. En cada uno de esos axes se pueden colocar información por separado.

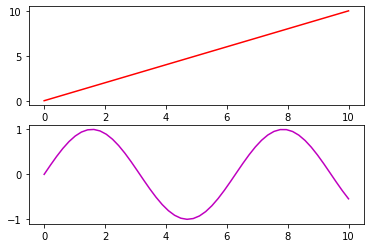
En el siguiente ejemplo se muestra el uso de la función subplot para crear dos axes apilados de forma vertical:

x = np.linspace(0,10)
y1 = x
y2 = np.sin(x)

plt.subplot(211)
plt.plot(x, y1, "r")

plt.subplot(212)
plt.plot(x, y2, "m")

[<matplotlib.lines.Line2D at 0x24ad5f03438>]

La sintaxis básica de subplot es:

plt.subplot(mnk)

Donde m corresponde al número de filas y n al número de columnas del arreglo de axes que se mostrarán. Observe que en el ejemplo anterior m=2 y n=1. El valor de k hace referencia a la posición (en el arreglo) del axes correspondiente. En ese entendido, la línea plt.subplot(211) refiere al axes en la primera posición del arreglo de dos filas y una columna, cualquier instrucción de graficado que se coloque posteriormente a esa línea, se entenderá que deberán mostrarse en ese axes, tal y como lo puede constatar en el ejemplo anterior.

Se pueden colocar etiquetas por separado a cada uno de los axes insertado mediante subplot, por ejemplo:

t = np.linspace(0,10)
s1 = t**2 + 1
s2 = 2*t

plt.subplot(211)
plt.plot(t, s1, "r")
plt.xlabel("Tiempo")
plt.ylabel("Posición")

plt.subplot(212)
plt.plot(t, s2, "m")
plt.xlabel("Tiempo")
plt.ylabel("Velocidad")

Text(0, 0.5, 'Velocidad')

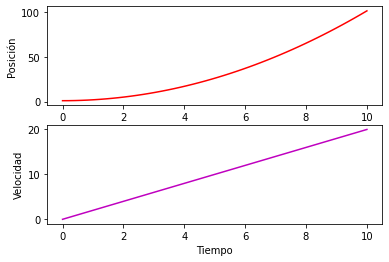
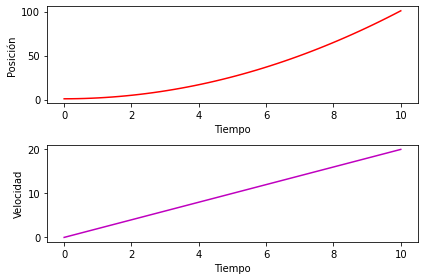
Se puede observar que, la etiqueta horizontal para el primer axes no es visible, esto se puede arreglar utilizando la función tight_layout:

t = np.linspace(0,10)
s1 = t**2 + 1
s2 = 2*t

plt.subplot(211)
plt.plot(t, s1, "r")
plt.xlabel("Tiempo")
plt.ylabel("Posición")

plt.subplot(212)
plt.plot(t, s2, "m")
plt.xlabel("Tiempo")
plt.ylabel("Velocidad")

plt.tight_layout()

Enseguida se muestra un conjunto de 16 axes creados con la función subplot, con la intención de que pueda indentificar el orden en el cual Matplotlib los coloca en la rejilla; se puede inferir rapidamente que los numera en orden creciente hacia la derecha y hacia abajo.

for k in range(1,17):
    plt.subplot(4,4,k)
    plt.text(0.5, 0.5, str(k), color="blue", fontsize=20)

plt.tight_layout()

Del código anterior se identifica que la función subplot también puede recibir los argumentos por separado, es decir, en la forma:

plt.subplot(m,n,k)

9.11. Gráficas de curvas paramétricas en el espacio¶

Una función vectorial de la forma:

\[\begin{split} \vec{r}(t) = \begin{bmatrix} x(t) \\ y(t) \\ z(t) \end{bmatrix} \end{split}\]

Se dice que es una función parámetrica, siendo \(t\) en este caso el parámetro correspondiente. Una función vectorial de este tipo tiene una curva en el espacio asociada como representación gráfica. Es muy común trabajar con este tipo de expresiones en el análisis cinemático de partículas.

Supongamos que queremos graficar la función vectorial:

\[\begin{split} \vec{r}(t) = \begin{bmatrix} \cos(t) \\ \sin(t) \\ t \end{bmatrix} \end{split}\]

En el intervalo \( 0 \leq t \leq 4\pi \). Para ello en Python haríamos lo siguiente:

from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")

t = np.linspace(0, 4*np.pi, 100)
x = np.cos(t)
y = np.sin(t)
z = t

ax.plot(x, y, z)

[<mpl_toolkits.mplot3d.art3d.Line3D at 0x20e72b32cc0>]

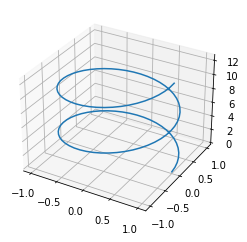
Ahora explicamos lo referente al código anterior. Observe que en la primera línea importamos la clase Axes3D del módulo mpl_toolkits.maplot3d, esto nos sirve para poder trabajar con gráficas tridimensionales. Luego, definimos un objeto de la clase Figure y lo asignamos a la variable fig, al objeto fig le añadimos un Axes mediante el método add_subplot, indicando que en dicho axes se utilizarán las proyecciones espaciales mediante el keyword argument projection. Las siguientes cuatro líneas definen las ecuaciones parámetricas. Y finalmente, con el método plot del objeto ax trazamos la gráfica de la curva tridimensional, note que en este caso el método plot, recibe al menos tres argumentos: las coordenadas en x, y, z.

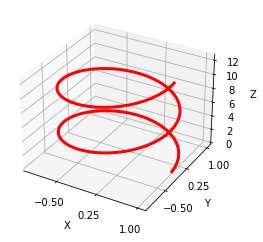
Al igual que en las otros tipos de gráficos, podemos también manipular las características. Vea por ejemplo el siguiente código:

fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")

t = np.linspace(0, 4*np.pi, 100)
x = np.cos(t)
y = np.sin(t)
z = t

ax.plot(x, y, z, color="r", linewidth=3)
xticks = ax.get_xticks()
yticks = ax.get_yticks()
ax.set_xticks(xticks[::3])
ax.set_yticks(yticks[::3])
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")

Text(0.5, 0, 'Z')

9.12. Gráficas de superficies¶

Las gráficas de superficies se utilizan para representar de manera gráfica una función bivariable en el espacio. El procedimiento de graficado para una función de dos variables \( z = f(x,y) \), implica que se tendría que evaluar dicha función en una región delimitada por ciertos valores para las dos variables independientes. Para poder realizar esto de forma muy conveniente, la librería NumPy proporciona una función llamada meshgrid, la cual puede crear una rejilla bidimensional a partir de una lista de valores para cada variable independiente, por ejemplo:

x = [0,1]
y = [10,20]
X,Y = np.meshgrid(x,y)
print(X,Y, sep="\n\n")

[[0 1]
 [0 1]]

[[10 10]
 [20 20]]

Las variables X y Y contienen arreglos bidimensionales que definen las coordenadas correspondientes de cada punto en la región a evaluar. Cada par ordenado \((x,y)\) se forma a partir de las posiciones correspondientes en las matrices X y Y. Se puede visualizar de forma muy sencilla los puntos en los cuales se evaluará la función \( f(x,y) \) utilizando la función plot:

plt.plot(X, Y, "o")

[<matplotlib.lines.Line2D at 0x20e72c5ec18>,
 <matplotlib.lines.Line2D at 0x20e72c5eba8>]

Observe que los puntos a evaluar en este caso serán \((0,10), (0,20), (1,10), (1,20)\). La densidad de la rejilla (o el número de puntos a evaluar) depende de la cantidad de valores que contengan los vectores que se le pasen como argumentos a la función meshgrid, por ejemplo:

x = [0,0.5,1]
y = [10,15,20]
X,Y = np.meshgrid(x,y)
plt.plot(X, Y, "o");

En general, si se requiere evaluar la funcion \( z = f(x,y) \) en la región \( R = \{(x,y)\,|\,a \leq x \leq b, c \leq y \leq d \} \), entonces se tendrá:

x = np.linspace(a,b,n)
y = np.linspace(c,d,n)
X,Y = np.meshgrid(x,y)

Donde n es un argumento que sirve para especificar el número de valores generados con linspace y en consecuencia servirá para controlar la densidad de la rejilla. Ahora, esas variables X y Y se pueden utilizar para formar expresiones matemáticas que correspondan a la función \( z = f(x,y) \).

Enseguida se muestra el código para graficar la superficie de la función \( z = x^2 + y^2 \), evaluada en la región \(R = \{(x,y)\,|\, -5 \leq x \leq 5, -5 \leq y \leq 5 \}\).

from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")

x = np.linspace(-5,5)
y = np.linspace(-5,5)
X,Y = np.meshgrid(x,y)
Z = X**2 + Y**2

ax.plot_surface(X, Y, Z, cmap="viridis");

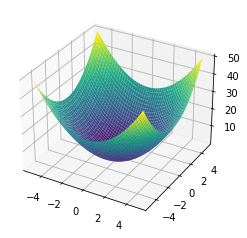
Desmenuzando un poco el código anterior, las primeras tres líneas, como se había descrito con anterioridad, sirven para poder crear un Axes que nos permita trabajar con gráficas tridimensionales. Con la función linspace se crean los intervalos de evaluación para cada variable independiente, luego, meshgrid permite formar la rejilla o puntos sobre los cuales se evaluará la función \( z = f(x,y) \). La expresión Z = X**2 + Y**2 es propiamente la evaluación de la función de dos variables. La función plot_surface recibe como argumentos las tres matrices X,Y,Z que corresponden a las variables independientes y función, respectivamente. El argumento cmap se utiliza para indicar el mapa de color que se utilizará.

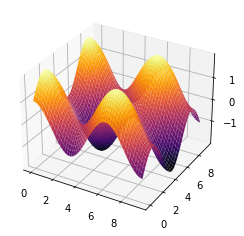
Enseguida se muestra otro ejemplo, en este caso se grafica la función \( z = \cos(x) + \text{sen}(y) \), evaluada en la región \(R = \{(x,y)\,|\, 0 \leq x \leq 3\pi, 0 \leq y \leq 3\pi \}\).

from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")

x = np.linspace(0, 3*np.pi)
y = np.linspace(0, 3*np.pi)
X,Y = np.meshgrid(x,y)
Z = np.cos(X) + np.sin(Y)

ax.plot_surface(X, Y, Z, cmap="inferno");

9.13. Ejercicios¶

Gráfique la función \( y = 10 \cos x \) en el intervalo \( 0 \leq x \leq 2\pi\)
Gráfique la función \( z = t^2 + \frac{1}{3}t \) en el intervalo \( -10 \leq t \leq 20\). Etiquete el eje horizontal como Tiempo y el eje vertical como Aceleración.
Gráfique la curva parámetrica:

\[\begin{split} x(t) = \cos t \\ y(t) = \text{sen } t \end{split}\]

Para \( 0 \leq t \leq 2\pi \)

8. NumPy: estructuras matriciales

10. SciPy

Python para Ingenieros